Yes, it is possible in theory. An important condition is that the mass of the potential satellite should be insignificant in comparison with the mass of the astronaut. A nut or a small pebble would be quite suitable for the role of a satellite for an astronaut.
Read also:
- It Is True That In Reality, Nobody Knows What Gravity Is? Then What Is Gravity?
- How Did They Take The First Image Of Earth From Space In 1946 if First Satellite Was Launched Only In 1957?
- Why Is The ISS Located At A Distance Of About 400 km From The Earth? Why Not 600 km, or 1000, or 300?
- If We Have To Provide Natural Oxygen In Spacecraft Then How Many Plants Would Be Needed?

The second important condition is the location of the astronaut. For example, when he is on the ISS, this situation is impossible. The fact is that every celestial body has a so-called Roche sphere.
Roche sphere is an area of space around an object, inside which it can hold a satellite, despite the influence of the gravity of that celestial body, it revolves around itself. The radius of the Roche sphere is calculated as follows:
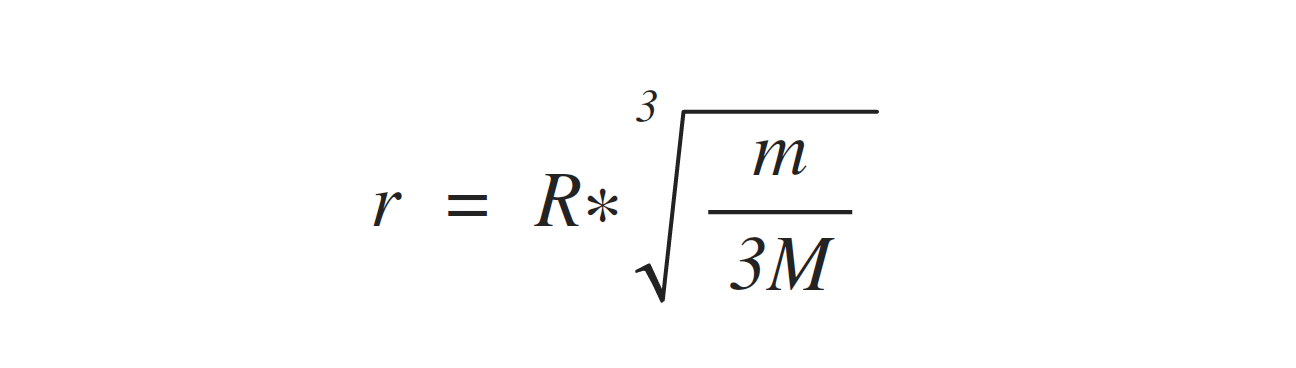
Substituting the numbers in the formula, it is easy to make sure that the radius of the Roche sphere for the astronaut in a spacesuit weighing 200 kilograms, in the orbit of the ISS (400 kilometers), the radius of the Roche sphere will be about 14 centimeters.
For the astronaut located at the orbit of the ISS, to capture and hold the satellite will not work: he is too big for this. All the orbits on which he could in theory hold the satellite are inside his body. In order to make it possible, either the astronaut must become a couple of centimeters in size while maintaining his mass, or move away from the Earth at a sufficiently large distance.
But if the astronaut is at the same distance from the Earth as the Moon (not in orbit around the Moon, but just at the same distance), then the radius of his Roche sphere will increase and become a little more than 8 meters. In this case, nothing will stop him from holding a small satellite in orbit around him.
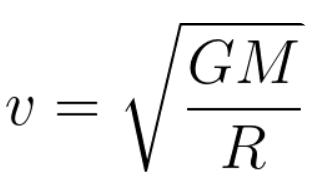
True, it is worth noting that the speed of rotation of such a satellite around the astronaut will be extremely small. This speed is determined by the formula, where M is the mass of the astronaut, R is the radius of the satellite’s orbit, G is the gravitational constant. Substituting the numbers in the formula, we get that around the astronaut in a spacesuit weighing 200 kilograms at a distance, 8 meters from the center of the astronaut, the satellite will have a speed of 0.000041 m/s. In order to make a complete revolution around the astronaut, such a satellite will need approximately 14 days, 6 hours, and 40 minutes. It will be impossible to notice the movement of such a satellite with the naked eye.








