When reading non-fiction literature on physics and cosmology, such as Stephen Hawking‘s “A Brief History of Time,” one can often see authors claiming that the universe is flat. What does it mean? Did the scientists suddenly believe in “the flat Earth theory” or anything else? How can the universe be both flat and volume? Let’s get it together.
Read also: “There Can Be Life In Another dimension:” Two-Dimensional Universes’ Secret
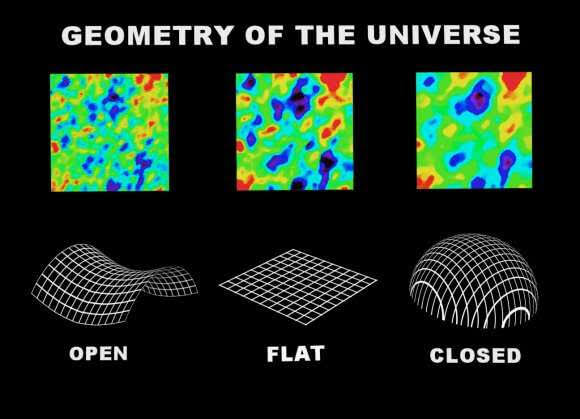
When astronomers and physicists say that the Universe is flat, they do not mean that the Universe is flat like a leaf. We are talking about the property of three-dimensional flatness – Euclidean geometry in three dimensions. In Euclidean astronomy, the world is a convenient comparative model of the surrounding space.
The substance in such a world is distributed uniformly, that is, in the unit, the volume contains the same amount of matter and is isotropic, that is, the distribution of matter is the same in all directions.
In addition, matter does not evolve there (for example, radio sources do not light up and supernovae do not flash), and space is described by the simplest geometry. This is a very convenient world for description, but not for living, since there is no evolution.
Read also: It’s True: Star ‘HD 140283’ Is Older Than The Universe
It is clear that such a model does not correspond to observational facts. The matter around us is distributed non-uniformly and anisotropically (somewhere there are stars and galaxies, and somewhere there are none), clusters of matter evolve (change over time), and space, as we know from the experimentally confirmed theory of relativity, is curved.
What is curvature in three-dimensional space?
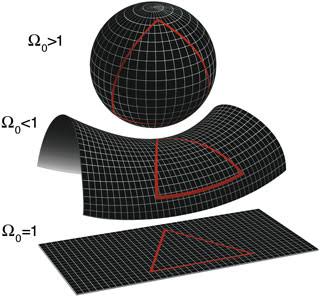
In the Euclidean world, the sum of the angles of any triangle is 180 degrees in all directions and in any volume. In non-Euclidean geometry, or in curved space, the sum of the angles of a triangle will depend on the curvature.
Two classic examples are a triangle on a sphere where the curvature is positive, and a triangle on a saddle-shaped surface where the curvature is negative. In the first case, the sum of the angles of the triangle is more than 180 degrees, and in the second case, it is less.
When we talk about a sphere or a saddle, we imagine curved two-dimensional surfaces surrounding three-dimensional bodies. When we talk about the Universe, we should understand that we are moving to the notion of three-dimensional curved space. For example, we are no longer talking about a two-dimensional spherical surface, but about a three-dimensional hypersphere.
Read also: We Are Created By Civilization With No Flesh And Bones: Here Is The Proof
So, why is the Universe flat in three-dimensional understanding if space is curved not only by clusters of galaxies, our Galaxy and the Sun but even the Earth?
In cosmology, the universe is considered as a whole object. And as an entire object, it has certain properties. For example, starting from some very large linear scales (60 megaparsecs [~ 180 million light-years], and 150 Mpc), matter in the Universe is distributed uniformly and isotropically. At smaller scales, clusters and superclusters of galaxies and voids between them are observed, that is, homogeneity is broken.
How can the flatness of the Universe as a whole be measured if the information on the distribution of matter in clusters is limited by the sensitivity of our telescopes?
It is necessary to observe other objects in a different range. The best thing that nature has given us is the cosmic microwave background, or relict radiation, which, having separated from the substance 380,000 years after the Big Bang, contains information about the distribution of this substance literally from the first moments of the existence of the Universe.
The curvature of the universe is associated with a critical density of 3H 2 / 8πG (where H is the Hubble constant, G is the gravitational constant), which determines its shape. The value of the parameter is very small – about 9.3×10-27 kg/ m³, or 5.5 hydrogen atoms per cubic meter.
This parameter distinguishes between the simplest cosmological models based on the Friedmann equations that describe the expanding Universe.
Cosmological parameters describing the density of the Universe (and the main ones are the density of dark energy, the density of dark matter and the density of baryonic [visible] matter) are expressed as a ratio to the critical density.
According to the observations of the Planck observatory , taking into account only relict radiation data (temperature, polarization and lensing), it was determined that the curvature parameter is very close to zero within small errors: Ω K = -0.004 ± 0.015, and taking into account data on the distribution of galaxy clusters and measurements of the expansion rate from the data on type Ia supernovae, the parameter Ω K = 0.0008 ± 0.0040. That is, the universe is flat with high accuracy.
Why is the Universe flatness important?
The flatness of the universe is one of the main pointers to the era of the very rapid expansion of the universe, described by the inflationary model. For example, at the time of the big bang, the Universe could have a very large curvature, while now, according to the CMB data, it is known that the universe is flat. The inflationary expansion makes it flat in the entire observed space (meaning, of course, large scales at which the curvature of space by stars and galaxies is not significant), just as an increase in the radius of the circle straightens the latter, and with an infinite radius, the circle looks like a straight line.








