Even in ancient times, people assumed that the Earth is flat. From the point of view of the ground observer, this is a pretty reasonable assumption because it looks like that, doesn’t it? No matter where you go, the planet will still look flat (excluding mountains and other landforms).
Read also:
- It Is True That In Reality, Nobody Knows What Gravity Is? Then What Is Gravity?
- Hollow Earth: Antarctica Could Be A Gateway To Another World Within The Earth
- Why Is The ISS Located At A Distance Of About 400 km From The Earth? Why Not 600 km, or 1000, or 300?
- Sorry, Elon Musk Lies To Us, There Is No Technology That Can Send Humans To Mars
But, as it turned out, if the observer continues to move in one direction, he will eventually return to the starting point. This will take some time, but it will be so. This is rather unusual. It would not have happened if the Earth was flat.
The earth looks flat only because the observer is extremely small, but on a large scale, the planet is folding.
What is the shape of the Earth in reality if it is not simply flat?
The answer is that the Earth’s surface is a two-dimensional manifold. This means that space is locally similar to Euclidean but may have a different global structure.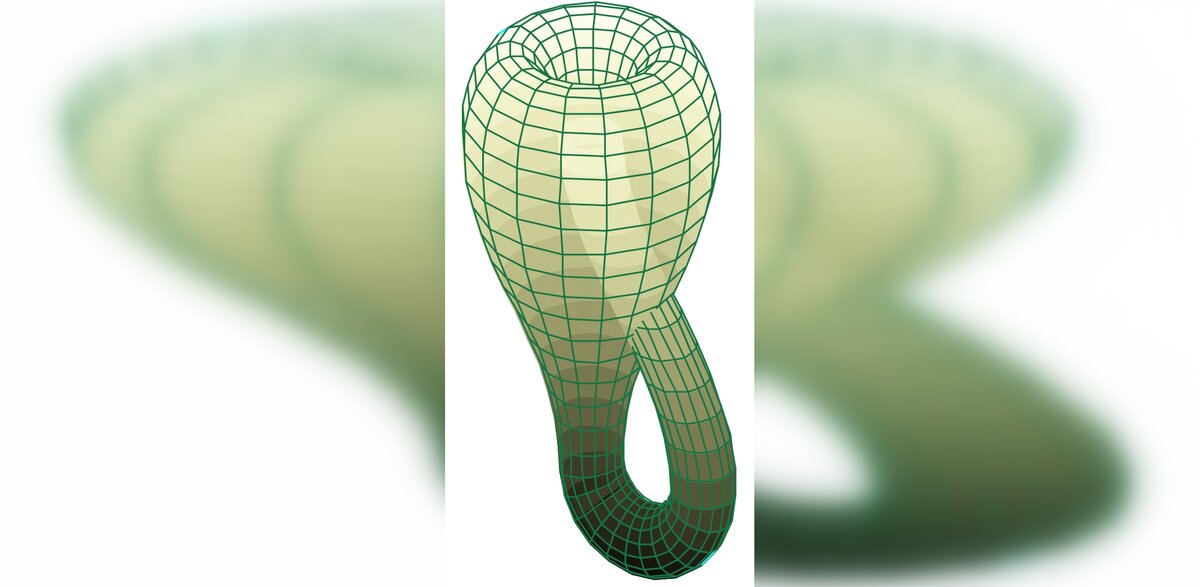
The earth might look like a donut, which in mathematics is called a torus, or the Earth could be in a weirder form, for example, like a Klein bottle.
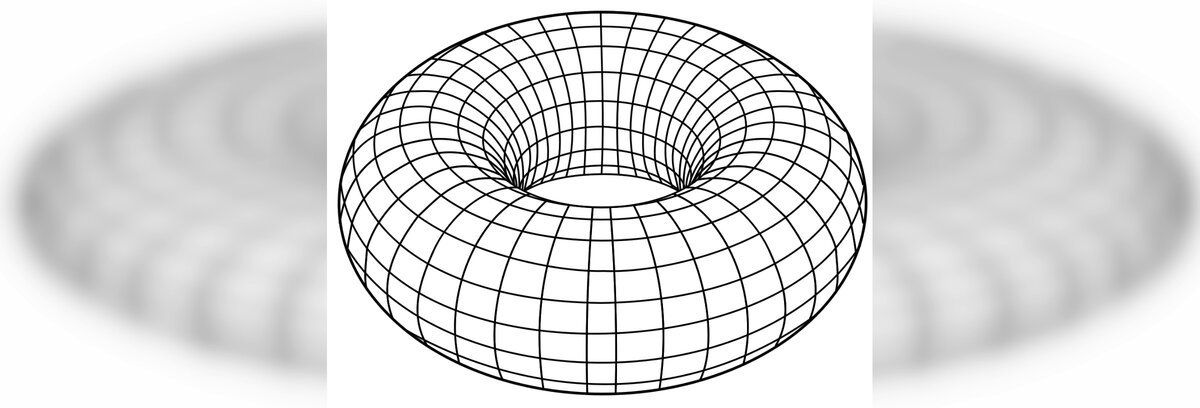
Notice how the two surfaces presented are conveniently divided into small rectangles linked together. It is known that an observer is much smaller than a rectangle. Therefore, being on one of them, it would be difficult for him to say that he was on a strange surface, as for him, it would be the same plane.
The observer would have to overcome gigantic distances and put all this down on the maps in order to clearly say on what surface he is moving.
In the general case, an n-dimensional space is locally similar to an n-dimensional Euclidean space, but on a large scale, it is built from many local ones.
Among other things, the universe is diverse. At the moment, it seems to be a kind of 3-dimensional.
In time, the Universe is a curved 4-dimensional manifold (Riemann, pseudo-Riemann), and curvature is gravity according to the general theory. Therefore, manifolds are important not only for mathematics but also for physics.








