Curvature is a few coherent concepts. In a general sense, this is the amount by which a curve deviates from a straight line or a surface deviates from a plane.
It is possible to calculate the magnitude of the curvature after knowing the average radius of the Earth (6371 km), trigonometric formulas, the Pythagorean theorem and correctly apply them, depending on the calculation method.
Read also:
- Voyager 1 Is located 22,300,000,000 km from Sun. Where Does It get Energy To Transmit Information To Earth?
- Where Did The Milky Way Images Come From If We Are Inside It?
- How Is It Possible That The Universe Extends To 93 Billion Light-Years If It Is Only 13.8 Billion Years Old?
- Is It Possible To Pick Up A Meteorite That Has Just Fallen?
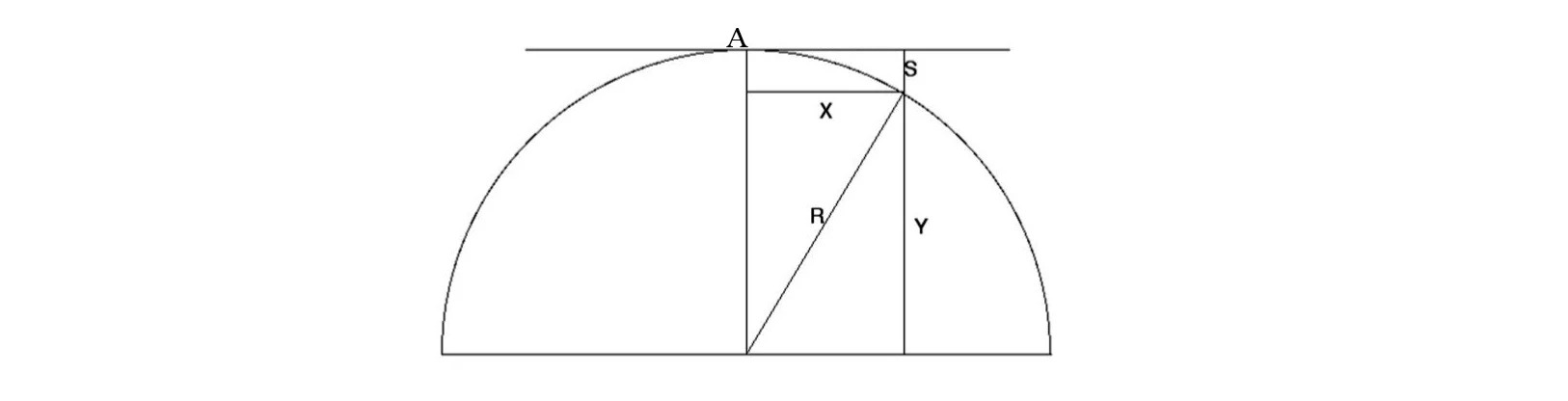
Earth’s curvature illustration
So, the magnitude of the earth’s curvature over a distance of one kilometer will be approximately 7.848 cm.
Let’s consider a little more in detail. To simplify, we believe that the terrain is perfectly flat. The observer looks from point A to the base of a tall object located, for example, 5 km from it.
In the first kilometer, the observation line will be below the eye level by 7.848 cm. In the second kilometer, the line is located at 31.392 cm below the level of the eyes that are at zero. In the fifth kilometer, as many as 1.96 meters of Earth’s curvature will obscure the base of the object.
The absolute height of the Mount Everest is 8848 meters. Given the curvature of our planet, from this peak, you can see the horizon at a distance of about 339 kilometers.
In clear weather, it is easy to observe an area of almost 3,60,000 sq.km. For comparison, countries such as Congo, Malaysia, Finland, Norway, Vietnam, Poland, Cote d’Ivoire occupy a little less.

The curvature of the planet was noticed a very long time ago and was reasonably clearly argued by the Greek scientist Eratosthenes around the 3rd century by using logic, geometry, and measurements.
But can anyone argue why the observer is looking from a high point, and the horizon is in all directions at the same level?
Just take any ball and a piece of thread or rope, in length compared to the scale distance by which you can see. Fix one end on one point of the ball. Then, holding the thread taut, rotate it relative to a fixed point. As a result, the limit horizon will be obtained.
The horizon appears flat no matter how high the observer is. But if you do this simple experiment, it becomes clear that the “flat” horizon, in this case, is on the sphere.
In fact, it is quite difficult to clearly recognize the curvature of the planet at the height of Everest, plus a piece of ice or rock, from which you can observe the horizon, is diluted with mountains and clouds. People are too small compared to the size of the Earth to see its curvature while on the surface.








